רבים מסתמכים על תואר שני במשפטים (LLM) גם לביצוע פעולות מתמטיות. גישה זו אינה עובדת.

הנקודה היא פשוטה: מודלים לשוניים גדולים (LLMs) לא באמת יודעים איך להכפיל. לפעמים הם יכולים לקבל את התוצאה הנכונה, בדיוק כמו שאני אולי יודע את הערך של פאי בעל פה. אבל זה לא אומר שאני מתמטיקאי, וגם לא ש-LLMs באמת יודעים איך לעשות מתמטיקה.

דוגמה מעשית

דוגמה: 49858 *5994949 = 298896167242 תוצאה זו תמיד זהה; אין דרך אמצע. זה נכון או לא נכון.

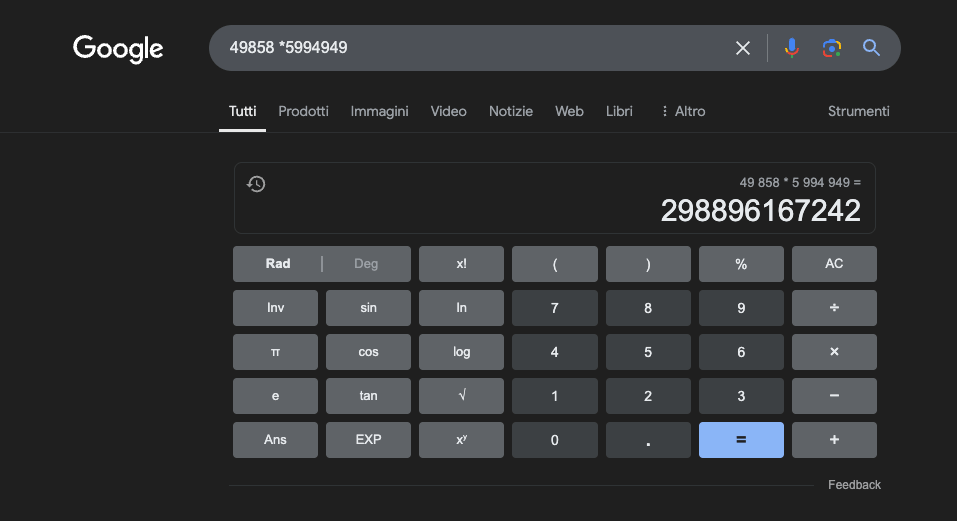
אפילו עם הכשרה מקיפה המתמקדת במתמטיקה, המודלים הטובים ביותר יכולים לפתור נכון רק חלק קטן מהחישובים. מחשבון כיס פשוט, לעומת זאת, משיג 100% מהתוצאות נכונות, בכל פעם. וככל שהמספרים גדולים יותר, כך הביצועים של המודלים לתואר שני גרועים יותר.

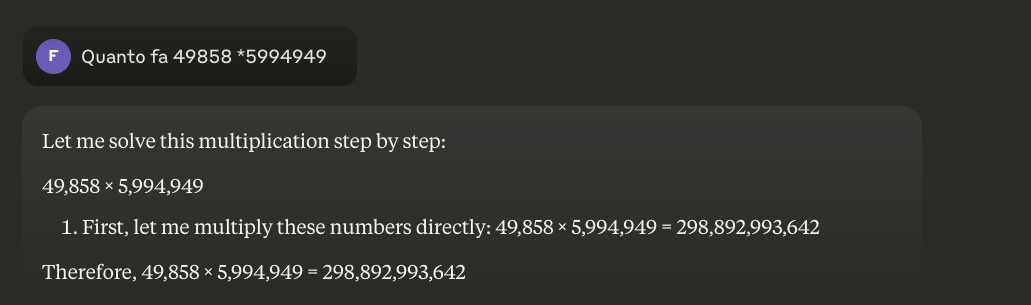
האם ניתן לפתור את הבעיה הזו?

הבעיה הבסיסית היא שמודלים אלה לומדים על ידי דמיון, לא על ידי הבנה. הם מתפקדים בצורה הטובה ביותר בבעיות דומות לאלה שעליהן אומנו, אך הם לעולם לא מפתחים הבנה אמיתית של מה שהם אומרים.

למי שרוצה ללמוד עוד, אני ממליץ על המאמר הזה בנושא " איך עובד תואר שני במשפטים ".

מחשבון, לעומת זאת, משתמש באלגוריתם מדויק שתוכנת לביצוע הפעולה המתמטית.

זו הסיבה שלעולם אסור לנו להסתמך לחלוטין על תוכניות לימודי משפטים (LLM) לחישובים מתמטיים: אפילו בתנאים הטובים ביותר, עם כמויות עצומות של נתוני אימון מיוחדים, הן לא מצליחות להבטיח אמינות אפילו בפעולות הבסיסיות ביותר. גישה היברידית עשויה לעבוד, אך תוכניות לימודי משפטים לבדן אינן מספיקות. אולי גישה זו תשמש לפתרון מה שנקרא "בעיית התות".

יישומים של תואר ראשון במשפטים (LLM) בלימודי מתמטיקה

בהקשר החינוכי, סטודנטים לתואר שני במשפטים יכולים לשמש כמדריכים מותאמים אישית, המסוגלים להתאים הסברים לרמת ההבנה של הסטודנט. לדוגמה, כאשר סטודנט מתמודד עם בעיית חשבון דיפרנציאלי, התואר השני יכול לפרק את ההיגיון לשלבים פשוטים יותר, ולספק הסברים מפורטים לכל שלב בתהליך הפתרון. גישה זו מסייעת לבנות הבנה מוצקה של מושגים בסיסיים.

היבט מעניין במיוחד הוא יכולתו של התואר השני במשפטים (LLM) לייצר דוגמאות רלוונטיות ומגוונות. אם סטודנט מנסה להבין את מושג הגבולות, התואר השני יכול להציג תרחישים מתמטיים שונים, החל ממקרים פשוטים ועובר למצבים מורכבים יותר, ובכך לאפשר הבנה הדרגתית של המושג.

יישום מבטיח אחד הוא השימוש בתואר ראשון במשפטים (LLM) כדי לתרגם מושגים מתמטיים מורכבים לשפה טבעית נגישה יותר. זה מקל על תקשורת המתמטיקה לקהל רחב יותר ועשוי לסייע להתגבר על המכשול המסורתי לכניסה לתחום זה.

תואר שני במשפטים (LLMs) יכול גם לסייע בהכנת חומרי הוראה, יצירת תרגילים ברמת קושי משתנה ומתן משוב מפורט על הפתרונות המוצעים על ידי התלמידים. זה מאפשר למורים להתאים אישית טוב יותר את מסע הלמידה של תלמידיהם.

היתרון האמיתי

באופן כללי יותר, חשוב גם לקחת בחשבון את ה"סבלנות" הקיצונית הנדרשת כדי לעזור אפילו לתלמיד הכי פחות מוכשר ללמוד: במקרה זה, היעדר רגש עוזר. למרות זאת, אפילו בינה מלאכותית לפעמים "מאבדת סבלנות". ראו דוגמה "משעשעת" זו.

‍